实验构建、指标计算、效果衡量都需要一些基础的统计学知识进行支撑
总体和样本
假设我们对全国人民的身高感兴趣,身高是我们关心的指标,全国人民是总体。总体的身高有一个分布,例如正态分布,刻画一个分布的参数很多,例如均值、方差、中位数等等。
在身高问题上,去测量每个人的身高然后得出总体的身高分布太昂贵也没有必要。在统计里面,我们通常会从所有人里面随机抽取一定数量的人,测量他们的身高,然后用他们的身高分布去推断总体的身高分布。这些随机抽取的人就是样本,样本中人的数量就是样本量,用样本的身高分布去推断总计的身高分布就是统计推断的核心内容,例如我们可以用样本均值去估计总体均值。
估计和假设检验
估计和假设检验是统计推断的两个主要的问题,统计推断都是针对总体参数的推断。为了简单起见,下面的描述都是针对总体均值这个参数。
估计包括点估计和区间估计。在身高问题中,假设样本的身高的平均值是$1.7m$,我们可以用$1.7m$去估计总体的身高的平均值,这就是点估计。样本的身高的平均值是从一个随机样本中计算出来的,因此它具有随机性,点估计不能体现出样本均值的随机性,因此我们通常也会对总体均值提供区间估计。区间估计通常伴随着统计的置信水平,例如95%。在身高问题中,我们可能计算出来的总体均值的95%的置信区间是$[1.68m, 1.72m]$。95%的置信区间可以这样理解,假设我们从总体中做了100次随机抽样,每次随机抽样我们都计算一个总体均值的95%的置信区间,这100个95%的置信区间有大概95个会包含总体均值。如果我们计算的是99%的置信区间,那么这100个99%的置信区间有大概99个会包含总体均值。直觉上,置信水平越高,置信区间越宽;给定置信水平,置信区间越宽,样本均值的随机性越大。
A/B实验的核心统计学理论是(双样本)假设检验。假设检验,即首先做出假设,然后运用数据来检验假设是否成立。需要注意的是 ,我们在检验假设时,逻辑上采用了反证法。通过A/B实验,我们实际上要验证的是一对相互对立的假设:原假设和备择假设。
- 原假设(Null Hypothesis $H_0$):是实验者想要收集证据予以反对的假设。A/B实验中的原假设就是指“新策略没有效果”。
- 备择假设(Alternative Hypothesis $H_1$):是实验者想要收集证据予以支持的假设,与原假设互斥。A/B实验中的备择假设就是指“新策略有效果”。
利用反证法来检验假设,意味着我们要利用现有的数据,通过一系列方法证明原假设是错误的(伪),并借此证明备择假设是正确的(真)。这一套方法在统计学上被称作原假设显著性检验 Null Hypothesis Significance Testing (NHST)。
在身高问题中,一对可能的假设可以是
- $H_0$: 总体身高均值是$1.7m$ VS $H_1$: 总体身高均值不是$1.7m$
在频率统计里面,我们通常假设$H_0$是对的,构建一个统计量,再把统计量转化成$P$值,$P$值越小,$H_0$不成立的可能性就越大,我们就越应该拒绝$H_0$。在假设检验里面,我们会范两类错误:第一类错误是$H_0$是对的我们拒绝$H_0$;第二类错误是$H_0$是错的我们接受$H_0$。两类错误相互冲突,即它们通常是往相反的方向移动,我们通常是控制第一类错误的概率,优化第二类错误的概率。为了控制第一类错误概率,统计显著性水平会在假设检验之前事先确定,例如5%,如果P值小于设定的显著性水平,我们就拒绝$H_0$,这样第一类错误的概率就是设定的统计显著性水平。
假设检验和置信区间有非常紧密的联系。在上面的假设检验问题里面,我们可以通过选择5%的显著性水平来把第一类错误的概率控制在5%,另外一种做法是计算总体身高均值的95%的置信区间,如果这个置信区间包含1.7m,我们就接受$H_0$,反之则拒绝$H_0$。这种做法的第一类错误的概率也是5%,原因很简单,如果$H_0$成立,即总体身高均值为$1.7m$,那么我们计算的置信区间会有95%的概率包含$1.7m$,所以95%的置信区间会有5%的概率不包含$1.7m$,而我们的决策方案是当置信区间不包含$1.7m$的时候拒绝$H_0$,因此这种依靠置信区间来做决策的第一类错误的概率也是5%。这也是为什么在A/B Test里面当$H_0$是对照版本和实验版本的均值相等的时候,我们可以看两个版本的绝对差的置信区间是否包含0来做出是否拒绝$H_0$的原因。
中心极限定理
显著性水平的理论依据便是中心极限定理。我们可以量化抽样误差的根基在于中心极限定理的存在。
由于存在抽样误差,我们每次实验所得到的指标结果,都可能与我们期望得到的真正结果有误差。假设我们从总体中抽取样本,计算其指标的均值,每一次计算,样本均值都会受抽样误差影响。假如我们做无数多次实验,那么理论上,这无数多个样本均值中,总应该有一个是“真的”,不受抽样误差影响的,这个值在统计学里被称为“真值”。
中心极限定理定告诉我们,如果我们从总体流量里不断抽取样本,做无数次小流量实验,这无数次抽样所观测到的均值,近似呈现正态分布(就是下图这样的分布)。这个分布以真值为中心,均值越接近真值,出现的概率就越大;反之均值越偏离真值,出现的概率就越小。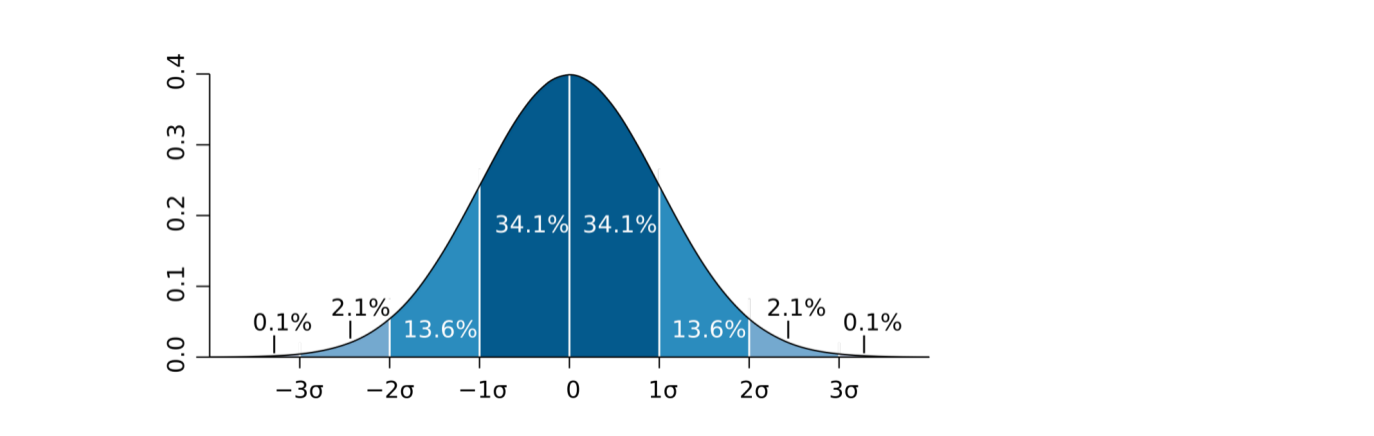
为什么样本均值越接近真值,出现的概率越大?
- 举个例子,如果从全中国人这个总体中,抽取很多很多次样本,计算很多很多次平均收入。
可以预见,我们会因为样本不同而得到很多个不同的平均收入值。这些数值确实有可能因为偶然抽到顶级富豪而偏高,或因为抽到极贫困的人口而偏低。但是,上述两种情况毕竟是少数(均值越偏离真值,出现的概率小)。随着抽样次数增多,我们会发现,平均收入落在大多数普通人收入范围内的次数,会显著增多(均值接近真值,出现的概率大)。并且,有了中心极限定理的帮助,我们可以知道每个均值出现的概率是多少。
P值和置信区间的计算
下面我们以CTR(点击率)指标来说明P值和置信区间如何计算。
假设计算CTR的单个样本点是用户,即先计算用户级别的CTR,然后再对所有的用户取平均。经常提到的UV_CTR每个样本点就是一个用户,在UV_CTR中, 每个曝光的用户取值是0(没有点击)或者1(点击);经常提到的PV_CTR每个样本点就不是一个用户,而是一次曝光,不同的曝光可能来自于同一个用户。为了把用户曝光的次数考虑进来,我们提出来计算UPV_CTR,即先对每个用户计算出一个CTR等于该用户的点击数除以曝光数,再取平均值。
下面的讨论围绕UPV_CTR进行,但是适用于任何单个样本点是用户的指标。
第二节里面的统计推断都是单样本的统计推断,在A/B Test里面,我们通常感兴趣的是实验版本和对照版本之间的比较,所以是两个样本的统计推断,好在大多数的情况下,实验版本和对照版本之间的样本是独立的,因此单样本的统计推断理清楚了,A/B Test里面的两个样本的统计推断自然也就清楚了。
假设对照版本和实验版本里面各有n个用户,假设对照版本里面n个用户CTR的值为 $x_1,…,x_n$;假设实验版本里面n个用户CTR的值为 $y_1,…,y_n$;用 $\mu_x$ 和 $\mu_y$ 分别代表对照版本和实验版本里面真实的UPV_CTR,在A/B Test里面我们通常关心两个参数:
- 两个版本指标的绝对差:$\mu_y - \mu_x$
- 两个版本指标的相对差:$(\mu_y - \mu_x)/\mu_x$
从假设检验的角度来说,不管关心哪个参数,$H_0$ 都是 $\mu_y = \mu_x$。从置信区间的角度来说,我们需要分别对绝对差和相对差提供区间估计。
在讲假设检验和区间估计的具体计算之前,定义如下的概念:
- 对照版本的样本均值:$\bar{x} = \displaystyle\sum_{i=1}^n{x_i}/n$
- 实验版本的样本均值:$\bar{y} = \displaystyle\sum_{i=1}^n{y_i}/n$
- 对照版本的样本标准差:$sd(x) = \sqrt{\displaystyle\sum_{i=1}^n(x_i - \bar{x})^2/(n - 1)}$
- 实验版本的样本标准差:$sd(y) = \sqrt{\displaystyle\sum_{i=1}^n(y_i - \bar{y})^2/(n - 1)}$
- 对照版本的样本均值的标准误差:$se(\bar{x}) = sd(x)/\sqrt{n}$
- 实验版本的样本均值的标准误差:$se(\bar{y}) = sd(y)/\sqrt{n}$
在假设检验中,定义t统计量为$(\bar{y} - \bar{x})/\sqrt{se(\bar{x})^2 + se(\bar{y})^2}$,再把$t$统计量通过与正态分布对比计算出$P$值。
在区间估计中,我们先设定好置信水平,通常为95%。绝对差的95%置信区间比较容易估计,具体的公式为:
相对差的置信区间比较麻烦,因为相对差的点估计为$(\bar{y}-\bar{x})/\bar{x}$,这个点估计的分子和分母都是随机的,因此之前约定的是在计算相对差的置信区间时假设$\bar{x}$的随机性可以忽略,这样我们可以先计算出$\mu_y$的置信区间,再用这个置信区间的上下界除以$\bar{x}$再减去1得到相对差的置信区间的上下界。具体的公式为:
如果考虑$\bar{x}$的随机性,相对差的置信区间应该如何计算呢?
此时需要更加严格的估计 $\bar{y}/\bar{x}$ 的方差:$\bar{y}/\bar{x}$ 更加严格的方差为: 。
定义: ,
则相对差的95%的置信区间为: 。